Contents
Minimum Execution Time Multiprocessor Scheduling Problem
To efficiently execute programs in parallel on a multiprocessor system, a minimum execution time multiprocessor scheduling problem must be solved to determine the assignment of tasks to the processors and the execution order of the tasks so that the execution time is minimized [E.Coffman76] .
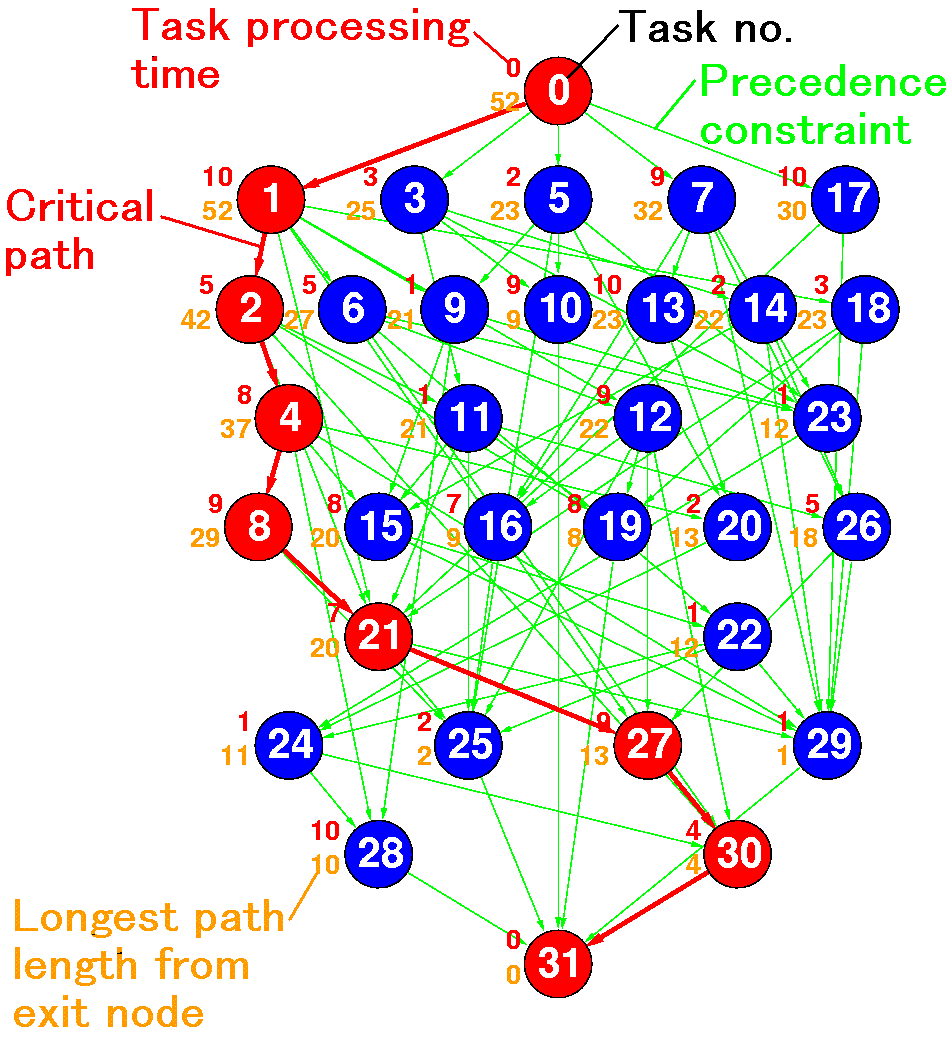
Figure 1 : A task graph
The multiprocessor scheduling problem treated in this project is to determine a non-preemptive schedule that minimizes the execution time, or the schedule length, when a set of n computational tasks having arbitrary precedence constraints and arbitrary processing time are assigned to m processors of the same capability. These tasks are represented by a directed acyclic graph (DAG) called a "task graph", G = (N, E), where N is the set of nodes (|N| = n is the number of nodes) and E is the set of edges (|E| = e is the number of edges), as shown in Figure 1. However, this problem has been known as strong NP-hard intractable optimization problem when it assumes arbitrary number of processors, arbitrary task processing time, and arbitrary precedence constraints (as shown in Table 1).
|
Number of Processors(m) |
Task Processing Time Ti |
Precedence Constraints |
Complexity |
|
Arbitrary |
Equal |
Tree |
O(n) |
|
2 |
Equal |
Arbitrary |
O(n^2) |
|
Arbitrary |
Equal |
Arbitrary |
NP-hard |
|
Fixed (m>=2) |
Ti=1or2 for all i |
Arbitrary |
NP-hard |
|
Arbitrary |
Arbitrary |
Arbitrary |
Strong NP-hard |
Standard Task Graph Set for Evaluation of Multiprocessor Scheduling Algorithms
The performance of scheduling algorithms has been evaluated using randomly generated task graphs [C.Ramamoorthy72] [H.Kasahara84] [T.Adam74] [A.Gerasoulis92] [T.Yang94] [H.El-Rewini90] [T.Yang93] [B.Shirazi90] [V.Almeida92] [G.Manimaran98] or task graphs modeled from actual application programs [T.Adam74] [A.Gerasoulis93] [T.Yang94] [Y.Kwok96] [B.Shirazi90] [H.Kasahara85] [S,Darbha98] [J.Llosa98] [A.Hurson90]. However, these task graphs are not typically available to other researchers. Therefore, fair performance comparisons of the algorithms under the same conditions has been impossible. To allow researchers to evaluate their algorithms under the same conditions, we proposed a Standard Task Graph Set covering previous task graph generation methods [C.Ramamoorthy72] [H.Kasahara84] [T.Adam74] [T.Yang91] [T.Yang94] [T.Yang93] [V.Almeida92].
|
Now the proposed
Standard Task Graph Set
is available at
To make the Standard Task Graph Set better, we welcome information or URL's about other task graphs. Please contact to |
References
- [E.Coffman76] E. G. Coffman, "Computer and Job-shop Scheduling Theory", John Willey & Sons (1976).
- [C.Ramamoorthy72] C. V. Ramamoorthy, K. M. Chandy and M. J. Gonzalez, "Optimal scheduling strategies in a multiprocessor system", IEEE Trans. Comput., Vol.C-21, No.2, pp. 137-146 (1972).
- [H.Kasahara84] H. Kasahara and S. Narita, "Practical Multiprocessor Scheduling Algorithms for Efficient Parallel Processing", IEEE Trans. Comput., Vol.C-33, No.11, pp. 1023-1029 (1984).
- [T.Adam74] T. L. Adam, K. M. Chandy and J. R. Dickson, "A Comparison of List Schedules for Parallel Processing Systems", Communications of the ACM, Vol.17, No.12, pp. 685-690 (1974).
- [A.Gerasoulis92] A. Gerasoulis and T. Yang, "A Comparison of Clustering heuristics for Scheduling Directed Acyclic graphs on Multiprocessors", J. of Parallel and Distributed Computing, Vol.16, pp. 276-291 (1992).
- [T.Yang94] T. Yang and A. Gerasoulis, "DSC : Scheduling Parallel Tasks on an Unbounded Number of Processors", IEEE Trans. Parallel and Distributed Systems, Vol.5, No.9, pp. 951-967 (1994).
- [H.El-Rewini90] H. El-Rewini and T. G. Lewis, "Scheduling Parallel Program Tasks onto Arbitrary Target Machines", J. Parallel and Distributed Computing, Vol.9, pp. 138-153 (1990).
- [T.Yang93] T. Yang and A. Gerasoulis, "List Scheduling With and Without Communication Delays", Parallel Computing 19, Vol.12, pp. 1321-1344 (1993).
- [B.Shirazi90] B. Shirazi, M. Wang and G. Pathak, "Analysis and Evaluation of Heuristic Methods for Static Task Scheduling", J. Parallel and Distributed Computing, Vol.10, pp. 222-232 (1990).
- [V.Almeida92] V. A. F. Almeida, I. M. M. Vasconcelos, J. N. C. Árabe and D. A. Menascé, "Using Random Task Graphs to Investigate the Potential Benefits of Heterogeneity in Parallel Systems", Proc. Supercomputing '92, pp. 683-691 (1992).
- [G.Manimaran98] G. Manimaran and C. Siva Ram Murthy, "An Efficient Dynamic Scheduling Algorithm for Multiprocessor Real-time Systems", IEEE Trans. Parallel and Distributed Systems, Vol.9, No.3 pp.312-319 (1998).
- [A.Gerasoulis93] A. Gerasoulis and T. Yang, "On the Granularity and Clustering of Directed Acyclic Task Graphs", IEEE Trans. Parallel and Distributed Systems, Vol.4, No.6, pp. 686-701 (1993).
- [Y.Kwok96] Y. Kwok and I. Ahmad, "Dynamic Critical-Path Scheduling: An Effective Technique for Allocating Task Graphs to Multiprocessors", IEEE Trans. Parallel and Distributed Systems, Vol.7, No.5, pp. 506-521 (1996).
- [H.Kasahara85] H. Kasahara and S. Narita, "Parallel Processing of Robot-Arm Control Computation on a Multiprocessor System", IEEE J. Robotics and Automation, Vol.RA-1, No.2, pp. 104-113 (1985).
- [S.Darbha98] D. Darbha and D. P. Agrawal, "Optimal Scheduling Algorithm for Distributed-Memory Machines", IEEE Trans. Parallel and Distributed Systems, Vol.9, No.1, pp. 87-95 (1998).
- [J.Llosa98] J. Llosa, M. Valero, E. Ayguadé and A. González, "Modulo Scheduling with Reduced Register Pressure", IEEE Trans. Comput., Vol.47, No.6, pp. 625-638 (1998).
- [A.Hurson90] A. R. Hurson, B. Lee, B. Shirazi and M. Wang, "A Program Allocation Scheme for Data Flow Computers", Proc. 1990 Int'l Conf. on Parallel Processing, pp. I-415-I-423 (1990).
- [T.Yang91] T. Yang and A. Gerasoulis, "A Fast Static Scheduling Algorithm for DAGs on an Unbounded Number of Processors", Proc. Supercomputing '91, pp. 633-642 (1991).
|
|
|
|